什么是正切函数？

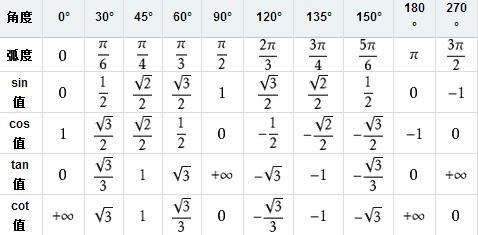
正切函数，通常用符号tan表示，是三角函数中的一种。它定义为直角三角形中，对边与邻边的比值。在数学中，正切函数是一个周期函数，其周期为π（即180度）。正切函数在直角三角形中的应用非常广泛，它可以帮助我们解决许多实际问题。

正切函数的定义

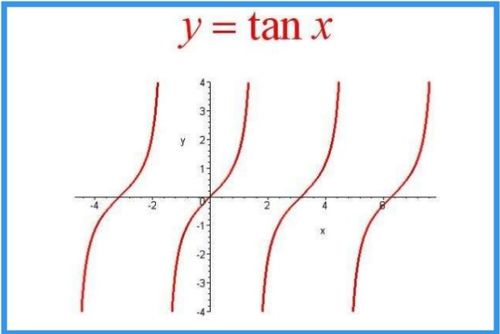
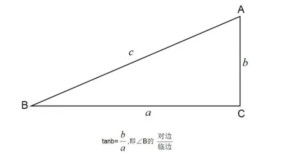
正切函数的定义可以表示为：在一个直角三角形ABC中，如果角A是直角，那么tan(A)=对边/邻边。这里的对边是指与角A相对的边，邻边是指与角A相邻的边。在直角坐标系中，我们可以用坐标来表示这个比值，即tan(θ)=y/x，其中θ是角度，x是x轴上的坐标，y是y轴上的坐标。

正切函数的性质

正切函数具有以下性质：

周期性：正切函数的周期为π，这意味着tan(θ)=tan(θ kπ)，其中k是任意整数。

奇函数：正切函数是一个奇函数，即tan(-θ)=-tan(θ)。

无界性：正切函数在定义域内是无界的，这意味着它的值可以无限大或无限小。

垂直渐近线：正切函数在θ=π/2 kπ（k为整数）时，函数值趋向于无穷大或无穷小，因此这些角度被称为正切函数的垂直渐近线。

正切函数的应用

物理：在物理学中，正切函数可以用来计算物体在斜面上的运动，例如斜面上的摩擦力。

工程：在工程设计中，正切函数可以用来计算斜率、角度等参数。

计算机图形学：在计算机图形学中，正切函数可以用来计算图像的缩放、旋转等变换。

导航：在航海和航空中，正切函数可以用来计算航向和速度。

正切函数的计算

使用计算器：大多数科学计算器都内置了正切函数的计算功能，可以直接输入角度或弧度来得到正切值。

使用三角恒等式：通过三角恒等式，可以将复杂的正切函数表达式简化为更简单的形式。

使用表格：在数学教学中，通常会提供正切函数的表格，通过查找表格中的值来得到正切函数的近似值。

正切函数的图像

正切函数的图像是一个波浪形的曲线，具有以下特点：

周期性：正切函数的图像在每个周期内重复。

垂直渐近线：图像在θ=π/2 kπ（k为整数）处有垂直渐近线。

无界性：图像在垂直渐近线两侧无限延伸。

正切函数是数学中一个重要的函数，它在许多领域都有广泛的应用。通过理解正切函数的定义、性质和应用，我们可以更好地利用这个函数来解决实际问题。在学习和使用正切函数时，了解其图像和计算方法也是非常重要的。